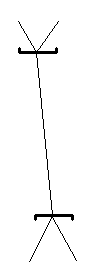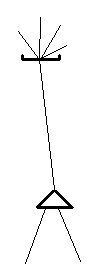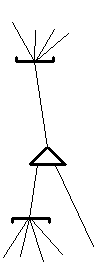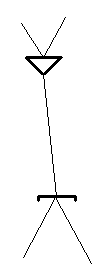Nection
A nection is the fundamental module of network structure in relational network theory. They are the regularly occurring modular structures in relational networks which are defined by having a central line connecting two nodes, one with upward branching, one with downward branching.
In More Detail
Refer to the images under "Examples" below to help you visualize the following:
- A line which connects the plural sides of two nodes (or the plural side of a node with a boundary of a network at which it interfaces with structure outside the network) may be called an external line.
- Any other line is an internal line. It follows that any internal line has at least one end connecting to the singular side of a node.
- Let us now say that on every external line there is a nection boundary. Or, we might say that the external line is the boundary, while also recognizing that that line belongs to both of the nections bounded by it.
Thus, a nection is a continuous portion of network (i.e. lines and nodes) bounded by nection boundaries.
A nection has one and only one line connecting the singular side of one node to the singular side of another node. This line may be called the nection center.
The nection is similar in form to various objects found in nature. Most familiar is a tree, with roots below and branches above. A river shows a similar form, with tributaries branching out into its higher elevations and a delta fanning out at its lowest. Notably, a neuron also has this form.
Examples
A nection for dog could be said to have lines connecting upward to nections for the lexemes lap-dog, underdog, hot dog, and puppy-dog, as well as to a nection for the conceptual category DOG; and lines connecting downward to each of three phonemes.
Here are examples of what a nection looks like in compact notation:
Properties
In order for the nection to be a valid model of a corresponding fundamental module in the cerebral cortex, then the following predictions must be found accurate:
- Varying degrees of activation
- Varying degrees of strength of connections
- Strengthening of connections as a learning process
- Local and distant excitatory connections
- Inhibitory connections
- Local only
- Two kinds: project either to line or to node
- Wait elements (needed for the ordered AND node)
- Bidirectional connections (feed-forward and feed-backward)
- Preponderance of latent connections
Sources
- LangBrain.
- Lamb, Sydney M.. 1999. Pathways of the Brain: The Neurocognitive Basis of Language. Philadelphia: John Benjamins.